A cyclic cellular automaton (CCA) is defined as an automaton where each cell takes one of N states 0, 1,…, N-1 and a cell in state i changes to state i+1 mod N at the next time step if it has a neighbor that is in state i+1 mod N, otherwise it remains in state i at the next time step. Classically CCA are applied on the 2-dimensional integer lattice with Von Neumann neighborhoods (nearest 4 neighbors): if cell is at coordinate (x,y), the four neighbours are those at coordinates (x+1,y), (x-1,y), (x,y+1), (x,y-1).
The cells are arranged in a bidimensional grid and initially they are in a random state. At each generation a cell in state i evolves to state i+1 mod N if at least one of its neighbors is in state i+1. The color of each cell is determined by its state.
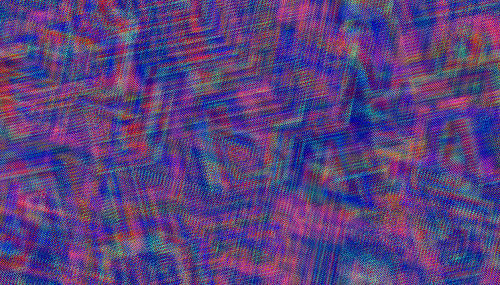
The following image is generated using Von Neumann neighborhood:
[click to enlarge]
For example using neighborhood (-2,-2), (3,-3), (-3,3), (5,5) we obtain the following image:
[click to enlarge]
With the Processing code below (that could be heavily optimized) you can experiment with different (and random) neighborhoods and colors. Let me know if you if you come up with other nice variants.
Other ideas that could be implemented:
- instead of starting from a random pattern, start from a grid of cells arranged in regular shapes (e.g. rectangles, circles, lines, …)
- use more neighbors (not only 4 neighbors), and also try to place them far apart
The code (you can also download it in zip format here):
/*
Cyclic Cellular Automata
https://www.algoritmarte.com/cyclic-cellular-automata/
Place the file CyclicCAplus.pde in a CyclicCAplus folder and double click
it (or Open it from Processing).
A cyclic cellular automaton (CCA) is defined as an automaton where
each cell takes one of N states 0, 1,..., N-1 and a cell in state i
changes to state i+1 mod N at the next time step if it has a neighbor
that is in state i+1 mod N, otherwise it remains in state i at the
next time step. Classically CCA are applied on the 2-dimensional
integer lattice with von Neumann neighborhoods (nearest 4 neighbors).
But very interesting behaviors can be obtained if we pick
irregular/random neighborhoods.
In the code below, the neighboughood is defined by the neighborhood array,
an array of pairs; each pair represents the relative coordinates of the neighbor;
for example {-1,-1} represents the top-left nearest neighbor.
Each time you press the 'c' key a new generation is started
with a new random neighborhood (which is printed, if you want to use it later).
If you press the space bar you change the color palette, but not the neighborhood.
The colors are picked randomly (subdivided in random monochromatic segments).
*/
/* ======================================== */
/* main parameters to experiment with .... */
// number of states of the cells (beware that if it's too big
// 4 neighbors are not enough to develop an evolving pattern
// (if it is greater than 24 you should also extend the number of neighbors)
static int CASTATES = 18;
// the neighbors of the central cells are define in the following array
// change it (and try also to add more points)
static int neighborhood[][] = {
{-2,-2}, {3,-3}, {-3,3}, {5,5}
//{-1,0}, {1,0}, {0,1}, {2,-2} // standard Von Neumann neighborhood
};
// the width of the cells (min. 1)
static final int CATILEW = 2;
// number of frames between every generation (larger values correspond to slower speed)
static final int EVOLVEEVERY = 4;
// a fixed central region of state 0 that doesn't evolve
// (leads to more interesting "refractions")
// set isledimension = 0 to disable it
int isledimension = 0;
/* ======================================== */
// other variables
static final int FPS = 30; // frames per second
// color array
int cacols[] = {0xFF2B0098,0xFF2B009A,0xFF2B009C,0xFF2B009E,0xFFCA00D4,0xFFCA00D6,0xFFCA00D8,0xFFC000BB,0xFFC000BD,0xFF420098,0xFF89003D,0xFF89003F,0xFF890041,0xFF39006F,0xFF390071,0xFF390073,0xFF2B00A8,0xFF2B00AA,0xFF00D960,0xFFD10087};
int cagrid[][][]; // two instances of a bidimensional grid
int caframe = 0;
int cawidth, caheight; // dimensions of the CA grid
boolean newCA = false;
int currcols[] = new int[cacols.length]; // current colors
// set this to true if you want to generate the frames for a video
static boolean recvideo = false;
static int videoduration = 300; // duration in seconds
static String videoframes = "D:/tmp/video/cycleca-######.tga";
/* ======================================== */
/*
Another nice combo:
Colors: {0xFFD700B0,0xFFCC0061,0xFFCC0061,0xFFE800E9,0xFFEA0080,0xFFEA0080,0xFFEA0080,0xFF7900E2,0xFF7900E2,0xFF001515,0xFFAB00E9,0xFFAB00E9,0xFFAB00E9,0xFFAB00E9,0xFF00CFFA,0xFF5B00EE,0xFF5B00EE,0xFF5B00EE};
Neighborhood: {{0,2};,{-3,7};,{-1,1};,{3,1};}
*/
/**
* Minimalistic setup
*/
void setup() {
frameRate( FPS );
size( 1280, 720 );
background(0);
cacols = new int[CASTATES];
changePalette(); // random palette
cawidth = width / CATILEW;
caheight = height / CATILEW;
cagrid = new int[2][cawidth][caheight];
for (int x = 0; x < cawidth; x++)
for ( int y = 0; y < caheight; y++)
cagrid[0][x][y] = irand(0,CASTATES-1);
printNeighborhood();
frame.requestFocus();
println( "Press SPACE to change palette" );
println( "Press 'c' to change nighborhood rules");
}
/**
* Change the palette
*/
static int mask[] = { 0xffff0000, 0xff00ff00, 0xff0000ff, 0xffffff00, 0xffff00ff, 0xff00ffff };
void changePalette() {
int n = 0;
while ( n < CASTATES ) {
int z = irand(1,3); // zone length (number of repeated colors for consecutive states)
int c = 0xff000000 | ( irand(10,0xff) << 16 ) | ( irand(10,0xff) << 8 ) | ( irand(10,0xff) << 0 );
int m = irand(0,mask.length*2-1);
if ( m < mask.length) c = c & mask[m]; // some sharpness :-)
for (int i = 0; i < z && n < CASTATES; i++ ) {
cacols[n++] = c;
}
}
String s = "Palette (cacols): {";
for (int i = 0; i < CASTATES; i++) s += ((i==0)? "" : ",") + "0x" + hex( cacols[i], 8 );
s += "};";
println( s );
}
void printNeighborhood() {
String s = "Neighborhood: {";
for (int i = 0; i < neighborhood.length; i++) s += ((i==0)? "" : ",") + "{" + neighborhood[i][0] +
"," + neighborhood[i][1] + "};" ;
s += "}";
println( s );
}
void randomCA() {
for (int i = 0; i < neighborhood.length; i++ ) {
//int i = irand( 0, pdirx.length-1);
neighborhood[i][0] = irand( -5, 5 );
neighborhood[i][1] = irand( -5, 5 );
}
for (int x = 0; x < cawidth; x++)
for ( int y = 0; y < caheight; y++)
cagrid[caframe][x][y] = irand(0,CASTATES-1);
printNeighborhood();
}
@Override
void mousePressed() {
//newCA = true;
}
@Override
void keyTyped() {
if ( key == ' ' ) changePalette();
if ( key == 'c' ) newCA = true;
}
/**
* Next generation
*/
void caevolve() {
int ev = 0;
int a = caframe;
int b = (caframe +1 ) % 2;
for (int x = 0; x < cawidth; x++) {
for ( int y = 0; y < caheight; y++) {
int v = cagrid[a][x][y];
int v1 = ( v + 1) % CASTATES;
for (int j = 0; j < neighborhood.length; j++ ) {
int tx = (x + neighborhood[j][0] + cawidth) % cawidth;
int ty = (y + neighborhood[j][1] + caheight) % caheight;
if (tx >= 0 && ty >= 0 && tx < cawidth && ty < caheight ) {
int vn = cagrid[a][tx][ty];
if ( vn == v1 ) {
v = v1;
ev++;
break;
}
}
}
cagrid[b][x][y] = v;
}
}
caframe = b;
if ( ev == 0 ) { // if there are no evolving cells, change some of them randomly
int p = 10 * (width * height) / 100;
for (int i = 0; i < p; i++ ) {
cagrid[caframe][ irand(0,cawidth-1)][ irand(0,caheight-1) ] = irand( 0, CASTATES - 1);
}
}
}
/**
* The drawing
*/
void draw() {
if ( newCA ) {
newCA = false;
randomCA();
}
if ( (frameCount % EVOLVEEVERY )==0) {
caevolve();
if ( isledimension > 0 ) {
int cx = cawidth / 2;
int cy = caheight / 2;
for (int x = 0; x < isledimension; x++) {
for (int y = 0; y < isledimension; y++) {
float d = abs(x) + abs(y);
if ( d < isledimension ) {
cagrid[caframe][ cx + x ][ cy + y ] = 0;
cagrid[caframe][ cx + x ][ cy - y ] = 0;
cagrid[caframe][ cx - x ][ cy + y ] = 0;
cagrid[caframe][ cx - x ][ cy - y ] = 0;
}
}
}
}
}
loadPixels();
for (int x = 0; x < width; x++) {
for ( int y = 0; y < height; y++) {
int cx = x / CATILEW;
int cy = y / CATILEW;
int p = x + y * width;
pixels[p] = currcols[ cagrid[caframe][cx][cy] ];
}
}
updatePixels();
for (int i = 0; i < cacols.length; i++ ) {
currcols[i] = fadecolToTargetAbs( currcols[i], cacols[i], 1 );
}
if ( recvideo ) {
if ( 1.0 * frameCount / frameRate < videoduration ) {
saveFrame( videoframes );
}
}
}
/**
* Add a fixed amount (rate) to the RGB components of the color
*/
int fadecolToTargetAbs(int c, int t, int rate ) {
if ( c == t ) return t;
int a = c & 0xff000000;
int r = (c & 0xff0000)>>16;
int g = (c & 0xff00)>>8;
int b = c & 0xff;
int ta = t & 0xff000000;
int tr = (t & 0xff0000)>>16;
int tg = (t & 0xff00)>>8;
int tb = t & 0xff;
if ( r > tr ) {
r -= rate;
if ( r < tr ) r = tr;
} else {
if ( r < tr ) {
r += rate;
if ( r > tr ) r = tr;
}
}
if ( g > tg ) {
g -= rate;
if ( g < tg ) g = tg;
} else {
if ( g < tg ) {
g += rate;
if ( g > tg ) g = tg;
}
}
if ( b > tb ) {
b -= rate;
if ( b < tb ) b = tb;
} else {
if ( b < tb ) {
b += rate;
if ( b > tb ) b = tb;
}
}
if ( r < 0) r = 0;
if ( g < 0) g = 0;
if ( b < 0) b = 0;
if ( r > 255) r = 255;
if ( g > 255) g = 255;
if ( b > 255) b = 255;
return ta | (r << 16) | (g << 8) | b;
}
/**
* Random int function
*/
int irand(int min, int max) {
if (max <= min) return min;
return min + round( random(0,1)*(max - min));
}